Post

PicoCTF | More Cookies

Writeup of a Web Exploitation Challenge from PicoCTF

Posted Updated
Preview Image
By Younes Tasra
10 min read
More Cookies is a web exploitation challenge worth 90 points.
This challenge is practically hard regradless of the point value. It is about performing a CBC Bit Flipping attack against an homomorphic encryption in order to find the bit responsible of identifying admin users from normal users, flip that bit and gain access as admin to eventually get the flag.

Description

Challenge Description

Discovery

  • We are presented with the following web page :
http://mercury.picoctf.net:34962/
  • Since the challenge title refers to Cookies, let’s check if there are some :
1

auth_name = L2M0a3lRaUd2bGNCcytsREhNTUNzSjhqQlQ3djljUCszeGl5RFlFdWlTQlc5b0c5ZW1IZzcvejZoeHBmeGNGOFpZRTdSUzFZMHR2eElhMnNXMi9IbHVBdTBVdE04T3hFbzZQcWlmQlVGQnZoWFhGVGRaWTQ2TnUzbVE4d1gxL0U=
  • We have a cookie called auth_name which seems to be base64 encoded.
  • Let’s base64 decode it using Cyberchef :
CyberChef
  • As you can see, the result also seems to be base64 encoded :
  • Let’s try decoding it one more time :
CyberChef
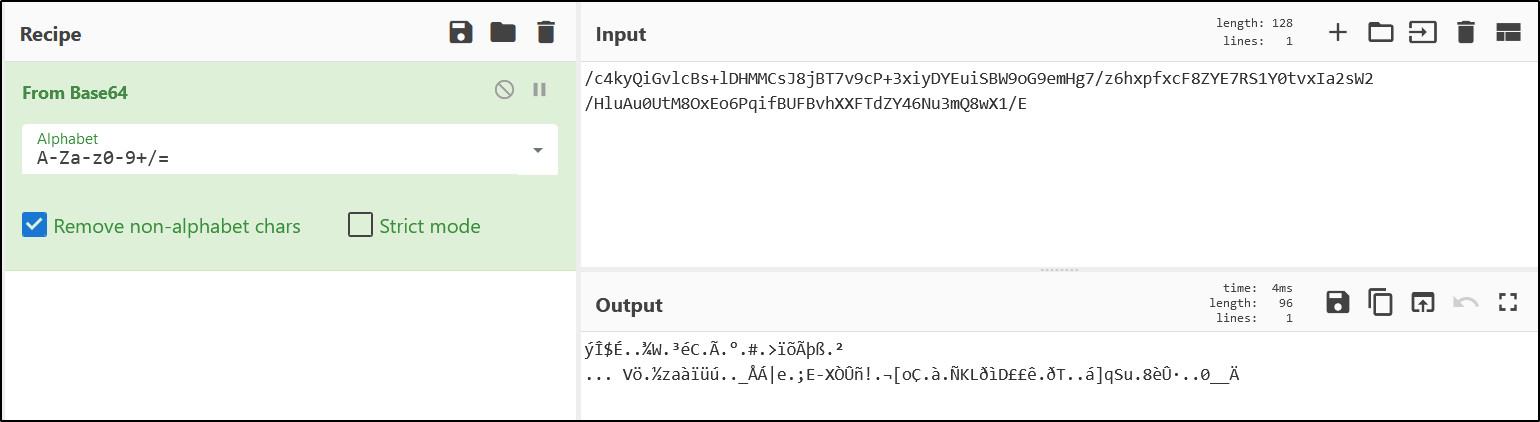
  • This time, we have some gibberish, unreadable piece of text.

  • This indicates that the cookie was encrypted, as per the challenge description, and base64 encoded twice

  • After taking a look af the first hint, which is a Wikipedia link, i realized that we are dealing with homomorphic encryption.

Homomorphic Encryption

As Per Wikipedia, Homomorphic Encryption is a form of encryption that permits users to perform computations on encrypted data without first decrypting it.

  • Basically, Homomorphic Encryption makes it possible to analyze and manipulate encrypted data without the need to decipher it and revealing private information.
  • To better understand the concept, let’s take the example of a person asking the location of a specific restaurant from a third party service.
  • This person is actually revealing a huge volumes of data (His current location, the fact that he wants a restaurant, what time it is and more …) with the service provider that’s going to locate for him the requested restaurant.
  • However, if homomorphic encryption was applied in this example, none of the revealed informations would be visible to the service provider such as Google.
  • With that being said, we need to find a way to manipulate the cookie without decrypting it in order to become an admin user.
  • Another thing worth mentioning is that, if you take a closer look at the Challenge Description, you will notice that the letters C, B and C are strangely capitalized, which is an indication that CBC or Cipher Block Chaining is the encryption scheme used to encrypt the Cookie.

Back to Basics

  • Before we can start tackling this problem, it’s worth revisiting how Cipher Block Chaining (CBC) works as we will need to understand how the algorithm operates in order to take on some advanced stuff.
  • Let’s start by defining some cryptographic algorithms :s

AES

  • AES, short for Advanced Encryption Standard, is a 128-bit symmetric bloc cipher, which means that it takes 128 bits of plaintext and encrypts it into 128 bits of ciphertext with a key that can either be 128, 192 or 256 bits.
  • AES comes with plenty of different modes, all labeled with a 3 letters names such as ECB (Electronic Code Book), CBC (Cipher Block Chaining), CTR (Counter) or CFB (Cipher Feedback) and more.

Block Cipher

  • A block cipher is a symmetric cryptographic algorithm that takes a plaintext block of length n and a key, and use that to generate a ciphertext block of the same length n.
  • AES is the most popular block cipher, as i mentioned earlier it operates on 128-bit blocks with keys of 128, 192 or 156 bits.
  • The problem here is that, if you have a file of 2GB and you are working with a 128-bit block cipher (AES for example), the algorithm is certainly not going to encrypt this large file in a single call.
  • This is where modes of operation comes into play.

ECB

  • ECB, or Electronic Codebook, is one of the solutions provided to overcome this problem.
  • The idea is to divide the data (plaintext) into multiple blocks and each block is encrypted separately using a block cipher algorithm with the same key.
Electronic Codebook (ECB) mode
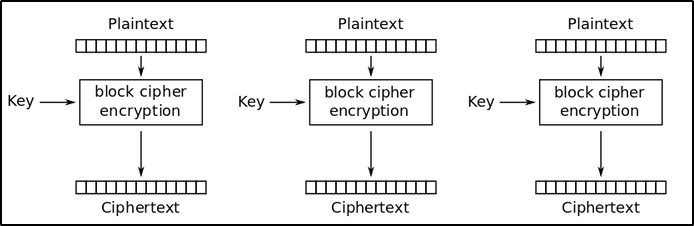
  • The problem with ECB mode is that encrypting the same block of plaintext always yields the same block of ciphertext.
  • This can allow the attacker to detect whether two ECB encrypted messages are identical, or share a common prefix or substrings.
  • Additionally, ECB mode is not semantically secure, which means that observing ECB encrypted ciphertext can leak informations about the plaintext.
  • Let’s take for example the following graphical demonstration i found on Wikipedia, where the same image is encrypted using both ECB mode and a semantically secure cipher mode like CBC:
ECB Penguin

CBC

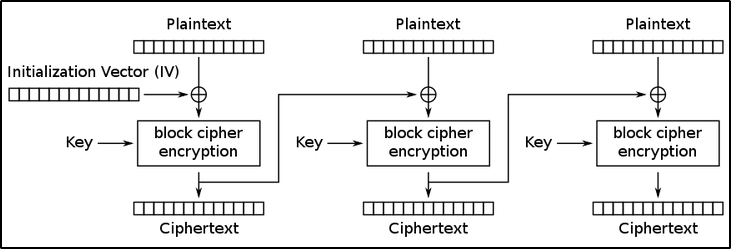
  • In CBC mode, each block of plaintext is XORed with the previous ciphertext block before being encrypted.
  • In other words, CBC mode links the output of one block to the input of the next block, which essentially randomise the encryption and hence generate distinct ciphertexts even if the same plaintext is encrypted multiple times.
  • For the first block, we use something called an Initialization Vector (IV), which is nothing more than a random array of bytes that has the same length of the blocks.
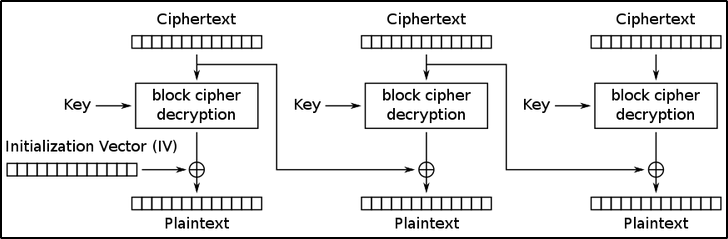
Cipher Block Chaining (CBC) mode Encryption
  • Decryption works by doing the process in reverse.
  • As you can see in the representation below, the first ciphertext block is decrypted using the decryption key (which is the same key used for encryption since we are working with symmetric encryption) and XORing the result with the Initialization Vector (IV), which gives us the first plaintext block.
  • Now, moving to the next block, we decrypt the second ciphertext block and XOR the result with the previous ciphertext block which gives us the second plaintext block
  • And So On …
Cipher Block Chaining (CBC) mode Decryption

Bit-Flipping Attack

  • Now that we understand how CBC works, we can now talk about Bit-Flipping attack.
  • The main vulnerable part of CBC is that, it relies on the previous ciphertext block in order to encrypt/decrypt the next plaintext/ciphertext block, and this is exactly where the Bit-Flipping attack comes into play.
  • Let’s see the visual representation of this attack in order to better understand how it works :
CBC Bit-Flipping Attack
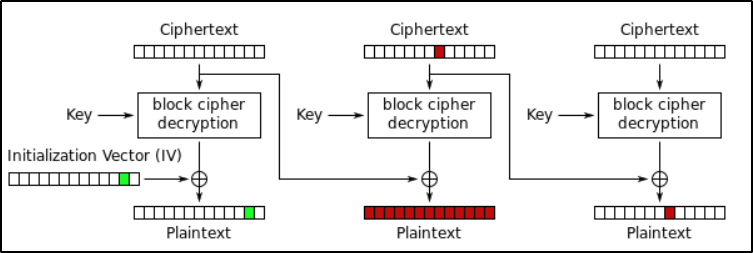
  • As you can see, a 1-bit error in the second ciphertext block :
    • Completely scambles the plaintext block which has the same index as the modified ciphertext;
    • AND Generates the same 1-bit error in the next plaintext block (Third block).
  • For example, in order to flip the first bit of the third plaintext block, we need to flip the first bit of the second ciphertext block.

Exploitation

  • Now that we have gone through the basics, let’s try to solve the challenge.
  • Since the challenge description highlights the use of AES-CBC mode to encrypt the auth_name cookie, we can assume that there is a bit, within the encrypted cookie, responsible of identifying admin users from normal users.

  • There is most likely a parameter like admin=0 and if we modify the proper bit, we can modify this parameter and set it to 1.

  • The problem is that the position of this particular bit is unkown, which means we need to try every single position and flip every single bit until the flag is shown.
  • To do so, let’s write a Python Script that will loop over all the bits in the cookie and flips each one until the flag is displayed.

Writing the exploit

  • First things first, let’s :
    1. Establish a session object using the requests module;
    2. Send a GET request;
    3. Grab the auth_name cookie and store it in a Cookie variable;
    4. Base64 decode twice the cookie.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

#!/usr/bin/python3

import requests
from base64 import *

Target = "http://mercury.picoctf.net:34962/"   # CHANGE THIS

# Create a session object :
session = requests.Session()

# Make a GET request :
session.get(Target)

# Storing the auth_name cookie in our Cookie variable :
Cookie = session.cookies["auth_name"]

# Base64 decode twice :
Raw_Cookie = b64decode(b64decode(Cookie))
  • At this point, if we print out Cookie and Raw_Cookie, we get the following :
1
2

Cookie: MEZJZWc5UGdIeUZqdVNMNGx0WXBiYk42WDBWSThaUW9hcW5zYjEzN2I2ckgyZVpTbG1wenRVbVNDb1VreG4xNHJOMExEL2Q2NTY5aEZpNlRGMndLMUVOL3d4cmxRRkhUS2Y0QTcxaWJPSVlseGU1d2NjS1VQakZzZUNheU82Rmk=
Raw_Cookie: b'\xd0R\x1e\x83\xd3\xe0\x1f!c\xb9"\xf8\x96\xd6)m\xb3z_EH\xf1\x94(j\xa9\xeco]\xfbo\xaa\xc7\xd9\xe6R\x96js\xb5I\x92\n\x85$\xc6}x\xac\xdd\x0b\x0f\xf7z\xe7\xafa\x16.\x93\x17l\n\xd4C\x7f\xc3\x1a\xe5@Q\xd3)\xfe\x00\xefX\x9b8\x86%\xc5\xeepq\xc2\x94>1lx&\xb2;\xa1b'
  • Now, let’s write the exploit where the Bit-Flipping process is going to take place.
    1. First, we define a loop to iterate over every single byte in the Raw_Cookie;
    2. Then, we define another nested loop to iterate over every single bit in the current byte of every iteration, given that every byte contains 8 bits (1-Byte = 8-bits);
    3. Then, we take every byte of every iteration and xor it with another byte where all bits are set to zero except the bit at the position ‘bit_index’ which going to be set to one;
    4. Base64 encode twice the generated cookie from the 3rd step;
    5. Send a GET request with the new cookie;
    6. Checking if the flag is displayed in the response;
      1. If so, printing out the flag, considering that the it is located between <code> and </code> HTML elements.
      2. Move on to the next byte and REPEAT.
  • Here is what our first and basic script will look like :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

#!/usr/bin/python3

import requests
from base64 import *

Target = "http://mercury.picoctf.net:34962/"        # CHANGE THIS

# Create a session object :
session = requests.Session()

# Make a GET request :
session.get(Target)

# Storing the auth_name cookie in our Cookie variable :
Cookie = session.cookies["auth_name"]

# Base64 decode twice :
Raw_Cookie = b64decode(b64decode(Cookie))

# Iterate over every single byte in the Raw_Cookie :
for byte_index in range(len(Raw_Cookie)) :

	# Iterate over every single bit in the current byte at the position "byte_index" => 1-Byte = 8-bits :
	for bit_index in range(0,8) :
		Potential_Raw_Cookie = Raw_Cookie[0:byte_index] + (Raw_Cookie[byte_index] ^ (1 << bit_index)).to_bytes(1, 'big') + Raw_Cookie[byte_index+1 :]
				
		# Base64 encode twice the Potential_Raw_Cookie to send out the Potential_Cookie in the same encoding scheme:
		Potential_Cookie = b64encode(b64encode(Potential_Raw_Cookie)).decode()	

		# Sending a GET request with the Potential_Cookie :
		r = requests.get(Target, cookies={"auth_name": Potential_Cookie})

		# Cheking if the response contains our flag format "picoCTF{" : 
		if ('picoCTF{' in r.text) :

			print("\n[*] HERE IS YOUR FLAG: " + r.text.split("<code>")[1].split("</code>")[0])
			exit()

# Clarification of the Potential_Raw_Cookie variable : +------------------------------------------------------------------------------------------+

		# Raw_Cookie[0:byte_index] 	 => All bytes before the current "byte_index", will not be engaged in the Bit-Flipping process, as they have already been tested.
		# Raw_Cookie[byte_index]   	 => This is the current byte where the Bit-Flipping is taking place.
		# 1 << bit_index           	 => This is the byte we created in order to xor it with the current byte, which is Raw_Cookie[byte_index]

			# if (bit_index == 0) then ( 1 << bit_index ) == 0000 0001 => 1
			# if (bit_index == 1) then ( 1 << bit_index ) == 0000 0010 => 2
			# if (bit_index == 2) then ( 1 << bit_index ) == 0000 0100 => 4
			# ...
			# if (bit_index == 7) then ( 1 << bit_index ) == 1000 0000 => 128
			
		# to_bytes(1, 'big')      	 => This will transfrom the XOR result into a raw format
		#            		  	 => For example, if the XOR result is 73 then to_bytes() will return b'\xe5'
		
		# Raw_Cookie[byte_index+1 :]	 => All bytes after the current "byte_index", will NOT YET be engaged in the Bit-Flipping process.	
#-------------------------------------------------------------------------------------------------------------------------------------------------+
  • The above script is very basic and simple, i wrote an improved and more verbose version, which walks you through the Bit-Flipping process and tells you where exactly it is taking place and makes you better understand the attack.

  • You can find it HERE.

  • The entire process can be see in the clip below :

References

https://crypto.stackexchange.com/questions/66085/bit-flipping-attack-on-cbc-mode/66086#66086

https://www.includehelp.com/cryptography/cipher-block-chaining-cbc.aspx

https://alicegg.tech/2019/06/23/aes-cbc.html

Challenges, PicoCTF
PicoCTF2021 Web Exploitation Cryptography AES AES-CBC AES-ECB xor Homomorphic Encryption Bit-Flipping Attack
This post is licensed under CC BY 4.0 by the author.